SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. broker25 |Heston, Lognormal, Lewis, SABR and CEV
- 15 августа 2014, 14:51
- |
Какая модель движения цены позволяет построить улыбку, наиболее близкую к рыночной?
Рассмотрим простой подход к выбору наилучшего метода.
Определение моделей
Для начала определим модели рынка.
a) Heston, Lognormal и Lewis.
В общем виде модель выглядит так.
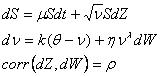
При λ = 0.5 получаем метод Хестона,
λ = 1 соответствует методу Lognormal,
λ = 1.5 соответствует методу Lewis’s 3/2.
Принимаем тренд равным нулю: μ = 0.
Неизвестные параметры:
θ — средняя долгосрочная волатильность;
η — vol of vol;
k > 0 - скорость сходимости текущей волатильности к средней;
ρ — коэффициент корреляции волатильности и БА;
б) Модель SABR
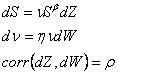
( Читать дальше )
Рассмотрим простой подход к выбору наилучшего метода.
Определение моделей
Для начала определим модели рынка.
a) Heston, Lognormal и Lewis.
В общем виде модель выглядит так.
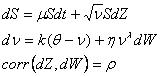
При λ = 0.5 получаем метод Хестона,
λ = 1 соответствует методу Lognormal,
λ = 1.5 соответствует методу Lewis’s 3/2.
Принимаем тренд равным нулю: μ = 0.
Неизвестные параметры:
θ — средняя долгосрочная волатильность;
η — vol of vol;
k > 0 - скорость сходимости текущей волатильности к средней;
ρ — коэффициент корреляции волатильности и БА;
б) Модель SABR
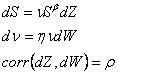
( Читать дальше )
- комментировать
- ★25
- Комментарии ( 17 )
Блог им. broker25 |Что такое рыночная улыбка волатильности?
- 27 января 2014, 15:48
- |
Под улыбкой волатильности каждый участник рынка понимает что-то свое. Сейчас мы поговорим о текущей рыночной улыбке. Той самой улыбке, которую биржа оценивает шестью загадочными параметрами. На самом деле, конечно, в природе никакой улыбки волатильности не существует. Есть набор бидов, оферов и последних цен. Откуда берется тогда точное значение волатильности в каждом страйке? Чтобы ответить на этот вопрос, нужно понять, зачем вообще нужна текущая улыбка? Я вижу три варианта ответа на этот вопрос
1. Маржа и ГО. Для биржи улыбка волатильности определяет теоретическую цену опционов, из которой выводятся вариационная маржа и ГО.
2. Оценка рыночной ситуации. Для трейдера улыбка определяет для каждого опциона возможную цену, по которой трейдер может провести сделку с поправкой на спред и проскальзывание. Зная исторические цены опционов и текущую цену, трейдер делает вывод о том, завышена или занижена цена дериватива, и принимает решение о сделке. Размерности биржевой улыбки часто не хватает, чтобы описать все зигзаги реальной рыночной кривой. В этом случае, если трейдер будет ориентироваться на биржевую улыбку, то будет удивлен, что его реальные цены сделок далеки от цен, предсказанных биржей. Если биды и офера рисуют кривую с тремя горбами, значит рыночная текущая улыбка для трейдера должна иметь три горба.
( Читать дальше )
1. Маржа и ГО. Для биржи улыбка волатильности определяет теоретическую цену опционов, из которой выводятся вариационная маржа и ГО.
2. Оценка рыночной ситуации. Для трейдера улыбка определяет для каждого опциона возможную цену, по которой трейдер может провести сделку с поправкой на спред и проскальзывание. Зная исторические цены опционов и текущую цену, трейдер делает вывод о том, завышена или занижена цена дериватива, и принимает решение о сделке. Размерности биржевой улыбки часто не хватает, чтобы описать все зигзаги реальной рыночной кривой. В этом случае, если трейдер будет ориентироваться на биржевую улыбку, то будет удивлен, что его реальные цены сделок далеки от цен, предсказанных биржей. Если биды и офера рисуют кривую с тремя горбами, значит рыночная текущая улыбка для трейдера должна иметь три горба.
( Читать дальше )
Блог им. broker25 |Выбор дельты для дельта-хеджа
- 26 декабря 2013, 15:34
- |
Изучение динамики улыбки подводит нас к другой важной теме – о выборе правильного метода дельта-хеджа. Какую волатильность использовать для расчета дельты — рыночную или расчетную? На конференции НОК-6 с интересным докладом на эту тему выступил Олег Мубаракшин. И опять я не был согласен с Олегом и теперь представляю свой подход к проблеме.
Способов расчета дельты много в зависимости от модели движения улыбки. Можно, взяв рыночную волатильность, считать дельту по БШ, можно делать коррекцию на движение улыбки и т.д. и т.п.
Как понять, какой способ лучше для расчета дельты? Как выбрать критерий для выбора? Критерий зависит от того, чего мы хотим от дельта-хеджа. Допустим, наша цель — минимальный размах ежедневных колебаний стоимости нашего портфеля. Тогда, наверно, в нашем тесте есть смысл минимизировать сумму квадратов ежедневных приращений стоимости портфеля. Предположим, мы желаем получить минимальный размах колебаний стоимости портфеля на экспирации. Соответственно, необходимо минимизировать
( Читать дальше )
Способов расчета дельты много в зависимости от модели движения улыбки. Можно, взяв рыночную волатильность, считать дельту по БШ, можно делать коррекцию на движение улыбки и т.д. и т.п.
Как понять, какой способ лучше для расчета дельты? Как выбрать критерий для выбора? Критерий зависит от того, чего мы хотим от дельта-хеджа. Допустим, наша цель — минимальный размах ежедневных колебаний стоимости нашего портфеля. Тогда, наверно, в нашем тесте есть смысл минимизировать сумму квадратов ежедневных приращений стоимости портфеля. Предположим, мы желаем получить минимальный размах колебаний стоимости портфеля на экспирации. Соответственно, необходимо минимизировать
( Читать дальше )
Блог им. broker25 |Зависимость IV от БА
- 23 декабря 2013, 20:40
- |
Волатильность возрастает при снижении базового актива? Вы уверены в этом? В мае этого года Олег Мубаракшин опубликовал статью Returns vs Volatility на эту тему, где изучал данный вопрос. На тот момент, у меня уже были аналогичные расчеты. С подходом и идеями Олега я не был согласен. Тем не менее, за отсутствием времени отложил свои возражения на потом. Сейчас я представлю свою точку зрения на этот вопрос.
Когда мы анализируем зависимость волатильности от БА, возникает соблазн сделать это в виде регрессии. В качестве зависимой переменной кажется логичным взять индекс волатильности или волатильность центрального страйка (IV(0)) в виде ряда чисел. Таким способом можно получить неточную зависимость и сделать неверные выводы. Я сейчас говорю не о расчетах Олега – возможно, он все сделал правильно – я говорю о своих ошибках в начале изучения этой темы.
Пусть, например, БА пошел вниз на один страйк, а улыбка не изменилась. Центральный страйк теперь другой, его волатильность выше. Разность текущей IV(0) и предыдущей положительна. Индекс волатильности в данной ситуации также вырастет. Можно сделать неправильный вывод, что волатильность растет при снижении БА. Но волатильность ни одного страйка не изменилась! Я решил проблему, фиксируя центральный и другие страйки на каждом шаге времени. При таком подходе можно четко увидеть рост или снижение волатильности конкретного страйка.
( Читать дальше )
Когда мы анализируем зависимость волатильности от БА, возникает соблазн сделать это в виде регрессии. В качестве зависимой переменной кажется логичным взять индекс волатильности или волатильность центрального страйка (IV(0)) в виде ряда чисел. Таким способом можно получить неточную зависимость и сделать неверные выводы. Я сейчас говорю не о расчетах Олега – возможно, он все сделал правильно – я говорю о своих ошибках в начале изучения этой темы.
Пусть, например, БА пошел вниз на один страйк, а улыбка не изменилась. Центральный страйк теперь другой, его волатильность выше. Разность текущей IV(0) и предыдущей положительна. Индекс волатильности в данной ситуации также вырастет. Можно сделать неправильный вывод, что волатильность растет при снижении БА. Но волатильность ни одного страйка не изменилась! Я решил проблему, фиксируя центральный и другие страйки на каждом шаге времени. При таком подходе можно четко увидеть рост или снижение волатильности конкретного страйка.
( Читать дальше )
Блог им. broker25 |Рисуем улыбку с помощью дельта-хеджа
- 19 декабря 2013, 13:16
- |
Продолжаю заумные, бесполезные и оторванные от жизни теоретические изыскания)) В этой статье я еще сильнее запутаю вопрос о улыбке опционов, наведу тень на плетень, запудрю мозги и напущу тумана))) Я покажу, что вопрос о форме улыбки еще сложнее, чем кажется тем, кто думает, что он сложный. В общем, я честно предупредил. Те, кто не хотят себя мучить, могут сразу перейти к выводам. Дисклеймер закончен, задержите дыхание — ныряем!
В последней статье «Улыбка недельных опционов» я вывел теоретическую улыбку на основании эмпирического распределения приращений индекса РТС. Является ли выведенная улыбка «справедливой»? Чтобы это проверить, нарисуем улыбку альтернативным способом — с помощью дельта-хеджа.
Также используем эмпирическое распределение пятидневных скачков базового актива. В качестве базового актива возьмем склеенный фьючерс на индекс РТС. Напомню, в прошлой статье базовым активом служил сам индекс. Здесь я использую дельта-хедж, хеджировать индекс нельзя, приходится использовать фьючерс. На результате, как будет видно далее, эта замена скажется не сильно.
( Читать дальше )
В последней статье «Улыбка недельных опционов» я вывел теоретическую улыбку на основании эмпирического распределения приращений индекса РТС. Является ли выведенная улыбка «справедливой»? Чтобы это проверить, нарисуем улыбку альтернативным способом — с помощью дельта-хеджа.
Также используем эмпирическое распределение пятидневных скачков базового актива. В качестве базового актива возьмем склеенный фьючерс на индекс РТС. Напомню, в прошлой статье базовым активом служил сам индекс. Здесь я использую дельта-хедж, хеджировать индекс нельзя, приходится использовать фьючерс. На результате, как будет видно далее, эта замена скажется не сильно.
( Читать дальше )
Блог им. broker25 |Толстые хвосты и эмпирические распределения. Продолжение
- 14 июня 2013, 11:32
- |
Продолжаю тему, поднятую в статье «Толстые хвосты и эмпирические распределения». Напоминаю, в материале рассматривался вопрос, как влияют толстые хвосты распределения цены базового актива на появление улыбки волатильности. В представленной модели фьючерс РТС каждый день прыгает на величину, случайно выбранную из ряда его ежедневных приращений в прошлом. Ранее были показаны результаты модели для 100 шагов движения цены. К ним мы еще вернемся, а пока рассмотрим, что происходит при небольшом количестве шагов модели. В этом случае, Центральная Предельная Теорема только начинает работать, и толстые хвосты разворачиваются во всей своей павлиньей красе.
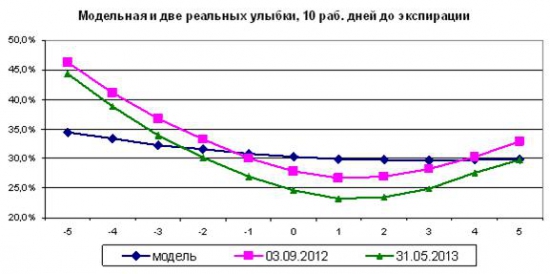
Выше представлена модельная улыбка за 10 дней и две реальных кривых волатильности опционов с аналогичным сроком жизни. Как и раньше, в модели введена поправка на тренд. По оси Х номер страйка от центрального, графики совмещены по горизонтали.
( Читать дальше )

Выше представлена модельная улыбка за 10 дней и две реальных кривых волатильности опционов с аналогичным сроком жизни. Как и раньше, в модели введена поправка на тренд. По оси Х номер страйка от центрального, графики совмещены по горизонтали.
( Читать дальше )
Блог им. broker25 |Толстые хвосты и эмпирические распределения
- 06 июня 2013, 15:15
- |
Финансовые рынки обладают известным свойством – толстые хвосты в распределении приращений актива. Обычно, для демонстрации эффекта сравнивают два графика дневной доходности – для исторического распределения цен и нормального. На рисунке ниже четко заметны выбросы в распределении доходности индекса вдалеке от центра.
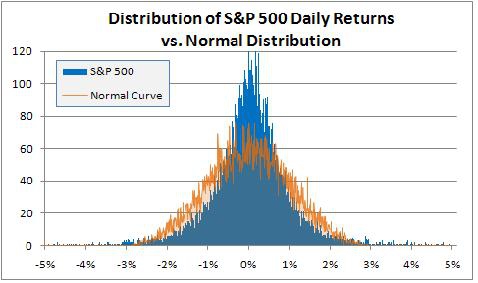
Часто можно услышать, как толстые хвосты назначают главной причиной возникновения улыбки волатильности. На недавно прошедшей НОК одним из наиболее интересных выступлений была презентация Виталия Курбаковского о причинах появления улыбки волатильности. Уважаемый мэтр строил улыбку на основе эмпирического распределения.
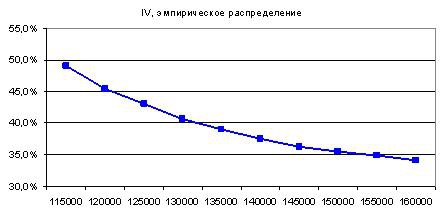
Проверим сами, как влияют толстые хвосты на форму улыбки. Построим модель движения фьючерса РТС на основе данных о ежедневной доходности close to close основной сессии. Возьмем ряд ежедневных приращений склеенного фьючерса с января 2010г. по февраль 2013г. Конечное значение цены близко к начальному, но, чтобы совсем исключить тренд, последнее значение цены фьючерса примем равным первому, а именно 157090 п. Период модели – 100 дней. Каждый день актив прыгает на величину, случайно выбранную из ряда прошлых значений. В конце траектории посчитаем стоимость опционов. Повторим опыт миллион раз. Усредним результаты каждого опыта и получим ожидаемую стоимость опционов в финальной точке. Она совпадает со справедливой стоимостью опционов в начальной точке, ведь ставка равна нулю. Результат моделирования в терминах волатильности представлен ниже
( Читать дальше )

Часто можно услышать, как толстые хвосты назначают главной причиной возникновения улыбки волатильности. На недавно прошедшей НОК одним из наиболее интересных выступлений была презентация Виталия Курбаковского о причинах появления улыбки волатильности. Уважаемый мэтр строил улыбку на основе эмпирического распределения.
Проверим сами, как влияют толстые хвосты на форму улыбки. Построим модель движения фьючерса РТС на основе данных о ежедневной доходности close to close основной сессии. Возьмем ряд ежедневных приращений склеенного фьючерса с января 2010г. по февраль 2013г. Конечное значение цены близко к начальному, но, чтобы совсем исключить тренд, последнее значение цены фьючерса примем равным первому, а именно 157090 п. Период модели – 100 дней. Каждый день актив прыгает на величину, случайно выбранную из ряда прошлых значений. В конце траектории посчитаем стоимость опционов. Повторим опыт миллион раз. Усредним результаты каждого опыта и получим ожидаемую стоимость опционов в финальной точке. Она совпадает со справедливой стоимостью опционов в начальной точке, ведь ставка равна нулю. Результат моделирования в терминах волатильности представлен ниже

( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лидеры роста и падения ммвб
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трейдер
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















